矩阵的加法计算器：从基础到应用的无缝之旅

矩阵的加法，这个看似简单的数学概念，实则蕴含了丰富的内涵。本文将带您深入了解矩阵加法的定义、起源、应用场景以及计算示例，让您在轻松的阅读中掌握这一重要的数学工具。

首先，让我们来揭开矩阵加法的神秘面纱。矩阵加法，顾名思义，是指对两个矩阵进行加法运算。具体来说，对于两个m×n矩阵A和B，它们的和是一个m×n矩阵C，其中C的元素cij=aij+bij。这个定义虽然简单，但它在数学和工程领域都有着广泛的应用。

那么，矩阵的加法究竟起源于何时何地呢？矩阵加法的起源可以追溯到19世纪中叶，当时英国数学家凯莱首次提出这一概念。随着时间的推移，矩阵加法逐渐成为线性代数领域的基础知识，为解决实际问题提供了强有力的工具。

了解了矩阵加法的定义和起源后，我们不禁要问：矩阵的加法有什么用呢？在实际应用中，矩阵加法具有广泛的应用场景。例如，在解决线性方程组时，我们可以利用矩阵加法对系数矩阵进行变换，从而简化方程组的求解过程。此外，在图像处理、信号处理等领域，矩阵加法也发挥着重要作用。

为了更好地理解矩阵加法的实际运用，我们可以看一个直观的计算示例。假设有两个2x2矩阵A = [1, 2; 3, 4] 和 B = [5, 6; 7, 8]，根据矩阵加法的规则，我们简单地将A和B对应位置上的元素相加得到结果矩阵C：

A + B = [1+5, 2+6; 3+7, 4+8] C = [6, 8; 10, 12]

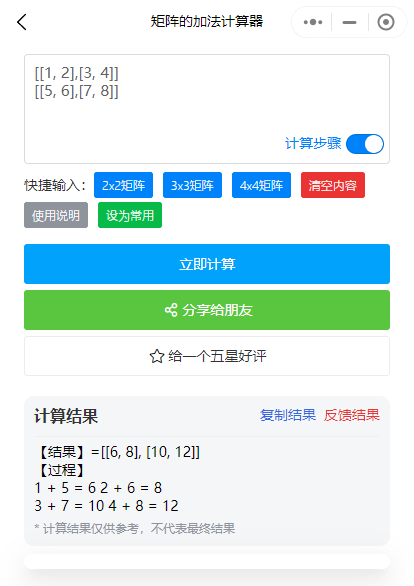
当然，要掌握矩阵加法，我们还需要了解其计算方法。矩阵的加法运算看似简单，但在实际操作中需要注意一些细节。例如，在进行矩阵加法时，我们需要确保两个矩阵是同型矩阵，即它们的行数和列数相等。此外，在进行元素相加时，我们需要遵循特定的运算法则，以确保计算结果的准确性。

总之，矩阵的加法作为线性代数中的基础概念之一，具有重要的理论和应用价值。通过本文的介绍，相信您对矩阵加法有了更深入的了解。希望本文能够帮助您更好地掌握这一知识点，并在实际应用中发挥其应有的作用。

——微信搜索【数学思维计算器】使用矩阵加法计算器